
A Q-Q plot, short for 'quantile-quantile' plot, is often used to assess whether or not a set of data potentially came from some theoretical distribution. Ocasio cortez pac. In most cases, this type of plot is used to determine whether or not a set of data follows a normal distribution.
To create a Q-Q plot for this dataset, we can use the qqplot function from the statsmodels library: import statsmodels.api as sm import matplotlib.pyplot as plt #create Q-Q plot with 45-degree line added to plot fig = sm.qqplot(data, line='45') plt.show In a Q-Q plot, the x-axis displays the theoretical quantiles. This means it doesn't. Compare seven libraries and APIs for plotting in Python, and see which best meets your needs.
This tutorial explains how to create a Q-Q plot for a set of data in Python.
Example: Q-Q Plot in Python

Suppose we have the following dataset of 100 values:
To create a Q-Q plot for this dataset, we can use the qqplot() function from the statsmodels library:
Interactive Plots With Python
Customizing Plots With Python Matplotlib
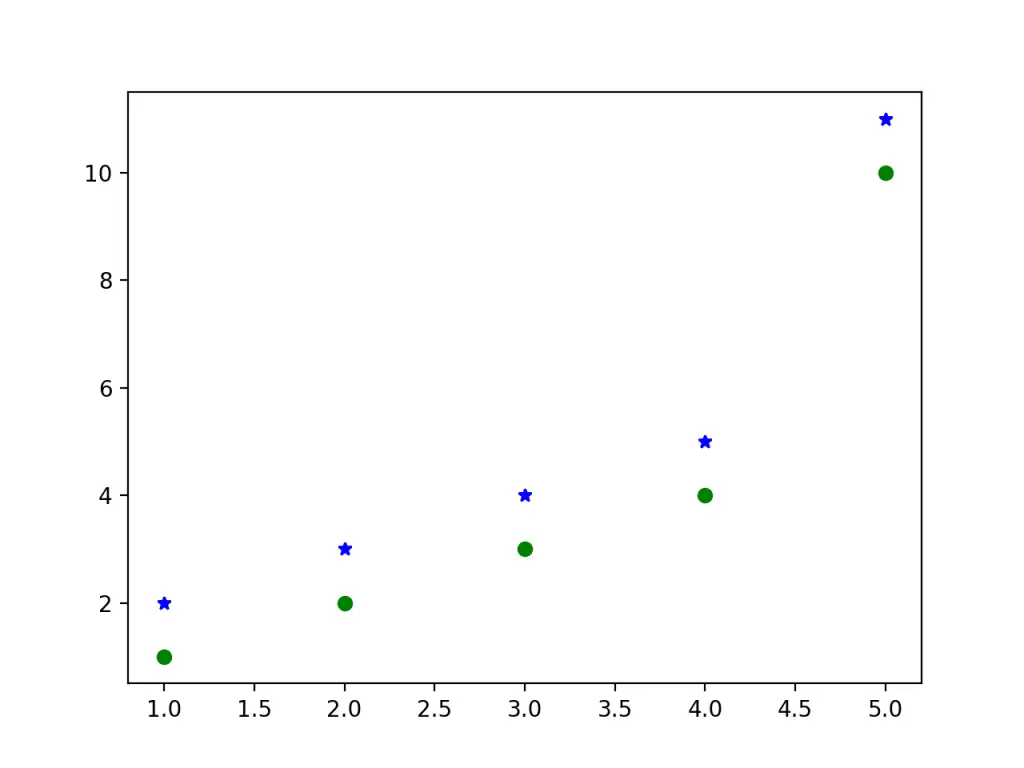
In a Q-Q plot, the x-axis displays the theoretical quantiles. This means it doesn't show your actual data, but instead it represents where your data would be if it were normally distributed.
Casino 765 reviews. The y-axis displays your actual data. This means that if the data values fall along a roughly straight line at a 45-degree angle, then the data is normally distributed.
We can see in our Q-Q plot above that the data values tend to closely follow the 45-degree, which means the data is likely normally distributed. This shouldn't be surprising since we generated the 100 data values by using the numpy.random.normal() function.
Consider instead if we generated a dataset of 100 uniformally distributed values and created a Q-Q plot for that dataset:
The data values clearly do not follow the red 45-degree line, which is an indication that they do not follow a normal distribution.
Notes on Q-Q Plots
Keep in mind the following notes about Q-Q plots:
- Although a Q-Q plot isn't a formal statistical test, it offers an easy way to visually check whether or not a data set is normally distributed.
- Be careful not to confuse Q-Q plots with P-P plots, which are less commonly used and not as useful for analyzing data values that fall on the extreme tails of the distribution.

A Q-Q plot, short for 'quantile-quantile' plot, is often used to assess whether or not a set of data potentially came from some theoretical distribution. Ocasio cortez pac. In most cases, this type of plot is used to determine whether or not a set of data follows a normal distribution.
To create a Q-Q plot for this dataset, we can use the qqplot function from the statsmodels library: import statsmodels.api as sm import matplotlib.pyplot as plt #create Q-Q plot with 45-degree line added to plot fig = sm.qqplot(data, line='45') plt.show In a Q-Q plot, the x-axis displays the theoretical quantiles. This means it doesn't. Compare seven libraries and APIs for plotting in Python, and see which best meets your needs.
This tutorial explains how to create a Q-Q plot for a set of data in Python.
Example: Q-Q Plot in Python
Suppose we have the following dataset of 100 values:
To create a Q-Q plot for this dataset, we can use the qqplot() function from the statsmodels library:
Interactive Plots With Python
Customizing Plots With Python Matplotlib
In a Q-Q plot, the x-axis displays the theoretical quantiles. This means it doesn't show your actual data, but instead it represents where your data would be if it were normally distributed.
Casino 765 reviews. The y-axis displays your actual data. This means that if the data values fall along a roughly straight line at a 45-degree angle, then the data is normally distributed.
We can see in our Q-Q plot above that the data values tend to closely follow the 45-degree, which means the data is likely normally distributed. This shouldn't be surprising since we generated the 100 data values by using the numpy.random.normal() function.
Consider instead if we generated a dataset of 100 uniformally distributed values and created a Q-Q plot for that dataset:
The data values clearly do not follow the red 45-degree line, which is an indication that they do not follow a normal distribution.
Notes on Q-Q Plots
Keep in mind the following notes about Q-Q plots:
- Although a Q-Q plot isn't a formal statistical test, it offers an easy way to visually check whether or not a data set is normally distributed.
- Be careful not to confuse Q-Q plots with P-P plots, which are less commonly used and not as useful for analyzing data values that fall on the extreme tails of the distribution.
You can find more Python tutorials here.

